we will proceed to solve each case to determine the solution
we have

case 1) f(0)= 0
For
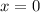
Find the value of f(x)


so

therefore
the statement case 1) is false
case 2) f(-2)= f(2)
For

Find the value of f(x)


For
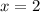
Find the value of f(x)


so

therefore
the statement case 2) is true
case 3) f(2) + f(5) = f(7)
For
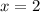
Find the value of f(x)


For
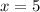
Find the value of f(x)


For
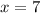
Find the value of f(x)


so

therefore
the statement case 3) is false
case 4) f(5) x f(2) = f(10)
For
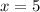
Find the value of f(x)


For
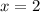
Find the value of f(x)


For

Find the value of f(x)


so

therefore
the statement case 4) is false
The answer is
