Question

What's the distance between equations y=2x+3 and y=2x-3

Answer 1

The distance between two parallel lines is the length of the perpendicular segment connecting the two lines.

We find the slope of the perpendicular:

`m_(perpendicular)=-(1)/(m)=-(1)/(2)`

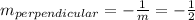
Pick a point on
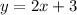
`y=2x+3` (let's go with
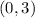
`(0, 3)`) and find where it intersects
`y=2x-3`

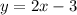
The perpendicular line will be
`y=-(1)/(2)x+3`

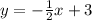
We have a system of equations:

`y=-(1)/(2)x+3`

`y=2x-3`
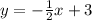
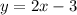
Solve:

`2x-3=-(1)/(2)x+3`
⇒
`(5)/(2)x-3=3`
⇒
`(5)/(2)x=6`
⇒
`5x=12`
⇒
`x=(12)/(5)`
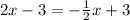
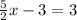
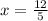
Plug into
`y=2x-3`:

`y=2((12)/(5))-3=(24)/(5)-(15)/(5)=(9)/(5)`

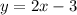
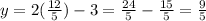
So our second point is
`((12)/(5), (9)/(5))`

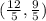
The distance between the points is:

`d=\sqrt{((12)/(5)-0)^(2)+((9)/(5)-3)^(2)}`
⇒
`d=\sqrt{((12)/(5))^(2)+(-(6)/(5))^(2)}`
⇒
`d=\sqrt{(144)/(25)+(36)/(25)}`
⇒
`d=\sqrt{(180)/(25)}`
⇒
`d=(√(180))/(5)`
⇒
`d=(6√(5))/(5)`

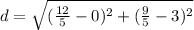
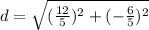
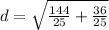
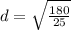
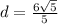
So the distance between the two lines is
`(6√(5))/(5)`

Answer 2

It is 6 as one of them is +3 and the other is -3, the difference between 3 and -3 is 6