Question

Find the locus of a point such that the sum of its distance from the point ( 0 , 2 ) and ( 0 , -2 ) is 6.

~Thanks in advance ! ​

Answer 1

`\displaystyle (x^2)/(5)+(y^2)/(9)=1`

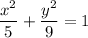
Explanation:

We want to find the locus of a point such that the sum of the distance from any point P on the locus to (0, 2) and (0, -2) is 6.

First, we will need the distance formula, given by:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

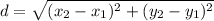
Let the point on the locus be P(x, y).

So, the distance from P to (0, 2) will be:

`\begin{aligned} d_1&=√((x-0)^2+(y-2)^2)\\\\ &=√(x^2+(y-2)^2)\end{aligned}`

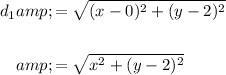
And, the distance from P to (0, -2) will be:

`\displaystyle \begin{aligned} d_2&=√((x-0)^2+(y-(-2))^2)\\\\ &=√(x^2+(y+2)^2)\end{aligned}`

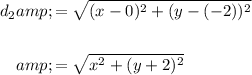
So sum of the two distances must be 6. Therefore:

`d_1+d_2=6`

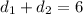
Now, by substitution:

`(√(x^2+(y-2)^2))+(√(x^2+(y+2)^2))=6`

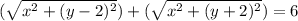
Simplify. We can subtract the second term from the left:

`√(x^2+(y-2)^2)=6-√(x^2+(y+2)^2)`

Square both sides:

`(x^2+(y-2)^2)=36-12√(x^2+(y+2)^2)+(x^2+(y+2)^2)`

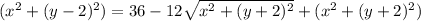
We can cancel the x² terms and continue squaring:

`y^2-4y+4=36-12√(x^2+(y+2)^2)+y^2+4y+4`

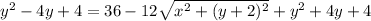
We can cancel the y² and 4 from both sides. We can also subtract 4y from both sides. This leaves us with:

`-8y=36-12√(x^2+(y+2)^2)`

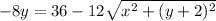
We can divide both sides by -4:

`2y=-9+3√(x^2+(y+2)^2)`

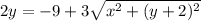
Adding 9 to both sides yields:

`2y+9=3√(x^2+(y+2)^2)`

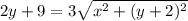
And, we will square both sides one final time.

`4y^2+36y+81=9(x^2+(y^2+4y+4))`

Distribute:

`4y^2+36y+81=9x^2+9y^2+36y+36`

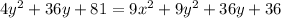
The 36y will cancel. So:

`4y^2+81=9x^2+9y^2+36`

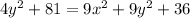
Subtracting 4y² and 36 from both sides yields:

`9x^2+5y^2=45`

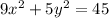
And dividing both sides by 45 produces:

`\displaystyle (x^2)/(5)+(y^2)/(9)=1`

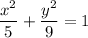
Therefore, the equation for the locus of a point such that the sum of its distance to (0, 2) and (0, -2) is 6 is given by a vertical ellipse with a major axis length of 3 and a minor axis length of √5, centered on the origin.