Question

The circulation time of a mammal (the average time it takes for all the blood in the body to circulate once and return to the heart) is proportional to the fourth root of the body mass of the mammal. Circulation time, T, is measured in seconds and body mass, m, is measured in kilograms.

(a) If the proportionality constant is 17.4, write a formula for the circulation time of a mammal. Use a lower case m.

(b) The body mass of a growing child is 38 kg and is increasing at a rate of 0.2 kg/month. What is the rate of change of the circulation time of the child? Round your answer to 3 decimal places.
_______sec/month

Answer 1

`T=17.4\sqrt[4]{m}`
Differentiate with respect to time
`s`:

`(dT)/(ds)=(17.4)/(4m^(3/4))(dm)/(ds)`
⇒
`(dT)/(ds)=(4.35)/(m^(3/4))(dm)/(ds)`
Plug in
`m=38` and
`(dm)/(ds)=0.2`:

`(dT)/(ds)=(4.35)/(38^(3/4))*0.2`
⇒
`(dT)/(ds)`≈
`0.057` sec/month

Answer 2

(a)
`T=17.4\sqrt[4]{m}`

(b) 0.057 sec/month.

Explanation:

Let T is the circulation time of a mammal in seconds and m is the body mass in kilograms.

It is given that the circulation time of a mammal is proportional to the fourth root of the body mass of the mammal.

`T\propto \sqrt[4]{m}`

`T=k\sqrt[4]{m}`

where k is constant of proportionality.

(a) The proportionality constant is 17.4. So, the circulation time of a mammal is

`T=17.4\sqrt[4]{m}`

(b)

The above equation can be written as

`T=17.4m^{(1)/(4)}`

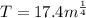
Differentiate with respect to time t.

`(dT)/(dt)=17.4((1)/(4)m^{(1)/(4)-1}(dm)/(dt))`

`(dT)/(dt)=4.35m^{-(3)/(4)}(dm)/(dt)`

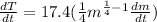
Substitute m=38 and
`(dm)/(dt)=0.2` in the above equation.

`(dT)/(dt)=4.35(38)^{-(3)/(4)}(0.2)`

`(dT)/(dt)=0.0568436`

`(dT)/(dt)\approx 0.057`

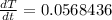
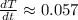
Therefore, the rate of change of the circulation time of the child is 0.057 sec/month.