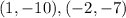Answer:
(-2, - 7), (1, -10)
Step-by-step explanation:
Two find any two points, we put in our desired values of x and solve to get the output
Let us choose x = - 2. Putting this value into the equation gives

simplifying the above gives

Hence, we have the point (-2, -7).
Now we choose x = 1 and put it into the equation:
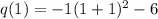
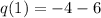
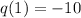
Hence, we have the point ( 1, -10).
To summarise, the two points we got are: