1 Answer

Fahd Arafat · Answer 1 · 2023-04-30T17:35:49+0000

Given:

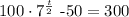
$100\cdot7^{(t)/(2)}\text{ -}50=300$

To solve the given problem, we add 50 to both sides first:

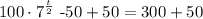
$\begin{gathered} 100\cdot7^{(t)/(2)}\text{ -}50+50=300+50 \\ \end{gathered}$

Simplify:

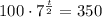
$100\cdot7^{(t)/(2)}=350$

Next, divide 100 by both sides:

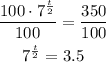
$\begin{gathered} \frac{100\cdot7^{(t)/(2)}}{100}=(350)/(100) \\ 7^{(t)/(2)}=3.5 \end{gathered}$

Then, we use the rule:

So,

$(t)/(2)=\log _73.5$

We multiply both sides by 2:

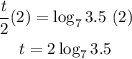
$\begin{gathered} (t)/(2)(2)=\log _73.5\text{ (2)} \\ t=2\log _73.5 \end{gathered}$

We can also use the base rule:

Thus,

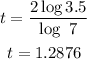
$\begin{gathered} t=\frac{2\log3.5}{\log\text{ 7}} \\ t=1.2876 \end{gathered}$

Therefore, the answer based on the given options are:

Step 1: Add 50 to both sides

Step 2: Divide 100 by both sides

Step 3:

Step 4: Multiply both sides by 2

Your comment on this question: