Given:
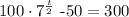
To solve the given problem, we add 50 to both sides first:
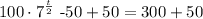
Simplify:
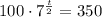
Next, divide 100 by both sides:
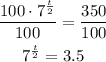
Then, we use the rule:
So,
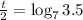
We multiply both sides by 2:
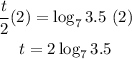
We can also use the base rule:
Thus,
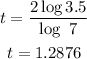
Therefore, the answer based on the given options are:
Step 1: Add 50 to both sides
Step 2: Divide 100 by both sides
Step 3:
Step 4: Multiply both sides by 2