Step-by-step explanation:
The polynomial is given below as
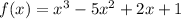
Since all coefficients are integers, we can apply the rational zeros theorem.
The trailing coefficient (the coefficient of the constant term) is
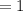
Find its factors (with the plus sign and the minus sign):
The factors will be

These are the possible values for p
The leading coefficient (the coefficient of the term with the highest degree) is
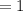
Find its factors (with the plus sign and the minus sign):
The factors will be

These are the possible values for q
Find all possible values of
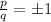
Next, check the possible roots: if aa is a root of the polynomial the remainder from the division will be zero
Check 1:
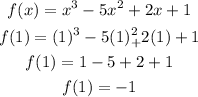
Check 2:
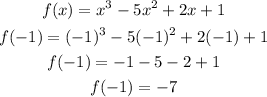
Hence,
The possible rational roots are

Hence,
This polynomial has no rational zeroes