Question

One of the fireworks is launched from the top of the building with an initial

upward velocity of 150 ft/sec.
a. What is the equation for this situation?
b. When will the firework land if it does not explode?
c. Make a table for this situation so that it shows the height from time
t = 0 until it hits the ground.
d. Calculate the axis of symmetry.
e. Calculate the coordinates of the vertex.
f. Explain why negative values for t and h t( ) do not make sense for this
problem.
g. On the same coordinate plane from #1, draw a graph that represent
for 25 ft

Answer 1

What about the Graph???

Explanation:

Answer 2

a. The height h of a firework launched from a building with an initial velocity
`(\(v_0\))` is given by
`\(h(t) = h_0 + v_0t - (1)/(2)gt^2\)`. b. The firework lands at
`\(t_1\)`. c. Table: t=0 to
`\(t_1\), \(h(t) = h_0 + v_0t - (1)/(2)gt^2\)`. d. Axis of symmetry:
`\(t = (v_0)/(g)\)`. e. Vertex:
`\(t = (v_0)/(g)\), \(h((v_0)/(g))\)`. f. Negative t and h(t) are non-physical. g. Graph: Plot points and vertex, connect smoothly; include point at h = 25.

a. The equation for the height of the firework as a function of time (\(t\)) can be modeled using the kinematic equation for free fall:

`\[ h(t) = h_0 + v_0 t - (1)/(2) g t^2 \]`

where:

- h(t) is the height at time t,

-
`h_0` is the initial height (height from which the firework is launched),

-
`\( v_0 \)` is the initial velocity (upward velocity of the firework),

- g is the acceleration due to gravity
`(\(32 \, \text{ft/s}^2\)` for Earth).

b. To find when the firework will land, set h(t) = 0 and solve for t.

c. Table:

`t & \quad h(t) \\0 & \quad h_0 \\t_1 & \quad 0 \quad \text{(time when the firework lands)}`

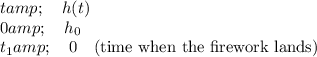
d. The axis of symmetry is the time at which the firework reaches its maximum height. For a projectile launched vertically, the axis of symmetry is given by
`\(t = (v_0)/(g)\)`.

e. The vertex represents the maximum height. To find the vertex coordinates, substitute the axis of symmetry time into the height equation.

f. Negative values for t and h(t) don't make sense because time and height cannot be negative in this physical context. Negative time doesn't have a physical interpretation, and negative height implies a position below the initial launch point, which is not meaningful for this problem.

g. To draw a graph for 25 ft, add the point
`\((t, h(t)) = (t_2, 25)\)` to the table, where
`\(t_2\)` is the time when the firework reaches a height of 25 ft. Plot these points and the vertex, and connect them with a smooth curve.