Question

What is the quotient: (2x2 + 10x + 12) ÷ (x + 3) ?

a. 2x + 6
b. 2x – 6
c. 2x + 4
d. 2x – 4, r = 1

Answer 1

The answer is C.  Factor the equation: 2x^2 + 10x + 12 which gives you............. 2(x + 2) (x + 3), and then cancel out (x + 3) because dividing (x + 3) by itself gives you one and the remaining term is 2(x +2) which is the same as 2x +4.

Answer 2

Answer: Option 'C' is correct.

Explanation:

Since we have given that

`f(x)=2x^2+10x+12\\\\and\\\\g(x)=x+3\\\\(2x^2+10x+12)/(x+3)`

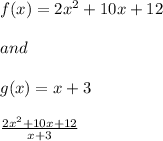
Now, we need to find the quotient of the given polynomial by dividing with g(x).

So, here we go:

Take out the common factor 2 from the numerator i.e. f(x), it becomes,

`2\left(x^2+5x+6\right)`

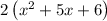
Now, we will apply the "Split the middle term", we get,

`\left(x^2+5x+6\right)\\\\=\left(x^2+2x\right)+\left(3x+6\right)\\\\=x\left(x+2\right)+3\left(x+2\right)\\\\=\left(x+2\right)\left(x+3\right)`

So, we will divide f(x) with g(x) :

`(2\left(x+2\right)\left(x+3\right))/(x+3)`

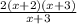
Now, Cancel out the like term :

So, we get

`2\left(x+2\right)\\\\=2x+4`

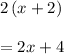
Hence, Option 'C' is correct.