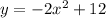Question

Find a quadratic model for each set of values (-1, 10), (2, 4), (3, -6)

Answer 1

A quadratic model has the general form:

`y=ax^2+bx+c`

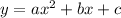
Since we are given three points, we can plug their x and y values into the general model of a quadratic equation to find a, b and c, like this:

`\begin{gathered} 10=a(-1)^2+b(-1)+c=a-b+c\text{ for the point (-1,10)} \\ 4=a(2)^2+b(2)+c=4a+2b+c\text{ for the point (2,4)} \\ -6=a(3)^2+b(3)+c=9a+3b+c\text{ for the point (3,-6)} \end{gathered}`

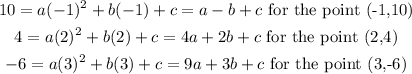
We can subtract the first equation from the second and get:

`\begin{gathered} 4-10=4a-a+2b+b+c-c \\ -6=3a+3b,\text{ dividing both sides by }3 \\ -2=a+b \\ a=-2-b \end{gathered}`

and subtracting the first equation third one, we get:

`\begin{gathered} -6-10=9a-a+3b+b+c-c \\ -16=8a+4b \\ -16-8a=4b,\text{ dividing both sides by 4} \\ -4-2a=b \end{gathered}`

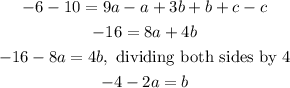
We can replace the equation b= -4-2a into the equation a= -2-b, and then find the value of a, like this:

`\begin{gathered} a=-2-b \\ a=-2-(-4-2a) \\ a=-2+4+2a \\ a-2a=-2+4 \\ -a=2 \\ a=-2 \end{gathered}`

Now that we know the value of a, we can replace it into b= -4-2a to calculate the value of b, like this:

`\begin{gathered} b=-4-2a \\ b=-4-2(-2) \\ b=-4-(-4) \\ b=-4+4=0 \end{gathered}`

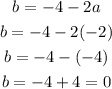
Then b equals 0, now we find the value of c with the equation of the point (-1,10), like this:

`\begin{gathered} 10=a-b+c \\ 10=-2-0+c \\ 10=-2+c \\ c=10+2=12 \end{gathered}`

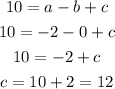
Then a= -2, b=0 and c=12, and the quadratic model of the set of values is:

`y=-2x^2+12`