Question

A population of beetles are growing according to a linear growth model. The initial population (week 0) is P0=4 , and the population after 6 weeks is P6=34 .

Answer 1

`\begin{gathered} P_n=4+5n \\ n=23 \end{gathered}`

EXPLANATION

Given:

`\begin{gathered} P_0=4 \\ P_6=34 \end{gathered}`

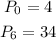
Desired Outcome:

1. Explicit formula (Pn)

2. Number of weeks the population of the beetle will reach 119

Note: This series is Arithmetic Progression with first term of P0 = 4

Now, let's determine the COMMON DIFFERENCE

`\begin{gathered} common\text{ }difference=(34-4)/(6) \\ =(30)/(6) \\ =5 \end{gathered}`

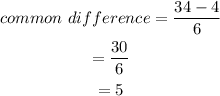
Therefore, every week 5 beetles are added.

The explicit formula becomes:

`P_n=4+5n`

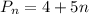
Determine the number of weeks the population of the beetles will reach 119

`\begin{gathered} P_n=119=4+5n \\ 119-4=5n \\ 115=5n \\ n=(115)/(5) \\ n=23 \end{gathered}`

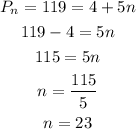
Hence, the number of weeks the population of the beetles will reach 119 is 23 weeks