Question

A 5.00-kg box slides 3.00 m across the floor before coming to rest. what is the coefficient of kinetic friction between the floor and the box if the box had an initial speed of 3.00 m/s?

Answer 1

The coefficient of kinetic friction between the floor and the box is μ = 0.1529

Explanation:

Let's start calculating the weight of the box.

Given that
`m=5.00kg` and gravity (g) is
`9.81(m)/(s^(2))` the weight is :

`W=m.g=(5.00kg).(9.81(m)/(s^(2)))=49.05N\\W=49.05N`

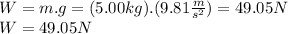
Given that the box is sliding across the floor, the normal force is
`49.05N`

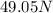
Now, the work that the frictional force produces is equal to the kinetic energy variation that the box experiments.

ΔKE = Work frictional force

ΔKE = KEfinal - KEinitial ⇒

If
`KE=(1)/(2)mv^(2)`

KEfinal = 0 J given that its speed is 0

ΔKE = KEfinal - KEinitial

ΔKE = 0 -
`(1)/(2)(5.00kg).(3.00(m)/(s))^(2)`

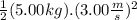
ΔKE = -22.5 J

The work that the frictional force produces is

Work frictional force = -(Frictional force).(distance)

The distance is 3.00 m

The frictional force is Nf.μ where Nf is the normal force and μ is the coefficient of kinetic friction between the box and the floor. We add a (-) given that the sense of the frictional force is opposite to the trajectory of the box.

Finally,

ΔKE = WFF

-22.5 J = - Nf.μ.d

μ =
`(22.5J)/((49.05N).(3.00m))=0.1529`

The coefficient of kinetic friction is 0.1529

Notice that this coefficient is dimensionless.