Question

Two tankers of equal mass attract each other with a force of 3.5 x 103 N. If their centres are 85 m apart, find the mass of each tanker.

Answer 1

6.15 · 10⁸ kg

Step-by-step explanation

Given:

• The force of attraction between the two tankers, F = 3.5x10³N

,

• The distance between their centers of mass, r = 85m

,

• The two tankers have equal masses, m₁ = m₂ = m

Known:

• The gravitational constant, G = 6.67 x 10⁻¹¹ Nm²/kg²

Unknown

• The mass of each tanker, m

By Newton's law of universal gravitation, we have that the force of attraction between two objects of masses, m₁, and m₂, separated by a distance r is,

`F=G\cdot(m_1m_2)/(r^2)`

In this case, both masses are equal,

`F=G\cdot(m^2)/(r^2)`

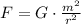
Solving for m,

`m=r\sqrt[]{(F)/(G)}`

Replace with the values,