Question

Given that P = (-5, 11) and Q = (-6, 4), find the component form and magnitude of vector QP.

PLEASE

Answer 1

Answer and Step-by-step explanation:

We see that the vector is written a QP.

Usually, when finding the vector in component form, it is in this form.

PQ = < q1 - p1,q2 - p2> = <v1,v2> = v

In this situation, Q and P are switched.

QP = < p1 - q1, p2 - q2> = <v1,v2> = v

Now, we plug in our values.

QP = < -5 - -6, 11 - 4 > = < 1 , 7 >

The component form of our vector is <1, 7>

To find the magnitude, we do this:

`||v|| = √((p1 - q1)^2 + ( p2 - q2)^2) = √((v1)^2+ (v2)^2)`

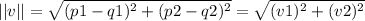
We already got the first part of this formula, so we plug in our vector into the second portion of the formula.

`||v|| = √((1)^2 + (7)^2) \\\\\\||v|| = √(1 + 49) \\\\\\||v|| = √(50) \\\\\\`

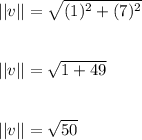
This simplifies down to
`2√(5)`, but the answer choice we are given shows
`√(50)`

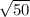
The magnitude of vector QP is
`√(50)`.

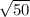#teamtrees #PAW (Plant And Water)

Answer 2

vector QP= (-5+6, 11-4) = (1, 7)
its magnitude is QP= sqrt( 1 + 49)= sqrt (50)=5sqrt2