Question

Find the area of an equilateral triangle with radius 4 sqrt 3m. Leave your answer in simpliest radical form.

Answer 1

Answer: The area of the equilateral triangle is 36√3 square meters.

Step-by-step explanation: We are to find the area of an equilateral triangle having the length of the radius equal to
`4\sqrt 3~\textup{meter}.`

We know that the area of an equilateral triangle having length of each side equal to 'a' units is given by

`A=(\sqrt3)/(4)a^2~\textup{sq. units.}`

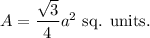
Now, the radius of an equilateral triangle is equal to two-third of the height of the trinagle.

So, if 'r' is the radius and 'h' is the height of the triangle, then we have

`r=(2)/(3)h~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

And, the height of the equilateral triangle with side length 'a' units is given by

`h=(\sqrt3)/(2)a.`

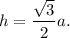
So, from equation (i), we have

`r=(2)/(3)* (\sqrt3)/(2)a\\\\\Rightarrow 4\sqrt3=(a)/(\sqrt3)\\\\\Rightarrow a=12.`

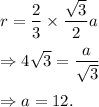
That is, side length, a = 12 meter.

Therefore, the area of the equilateral triangle is given by

`A\\\\\\=(\sqrt3)/(4)a^2\\\\\\=(\sqrt 3)/(4)(12)^2\\\\\\=36\sqrt3~\textup{sq. meters.}`

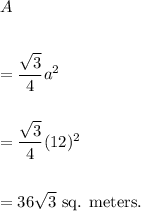
Thus, the area of the equilateral triangle is 36√3 square meters.

Answer 2

Correct answer is
`36√(3)`

The radius of an equilateral triangle is equal to 2/3 of the height.


`R= (2)/(3) h= (2)/(3) (a √(3) )/(2) = (a √(3) )/(3) \\4 √(3)= (a √(3) )/(3) \\3* 4√(3)=a √(3) \\a=12 \\ \\A= (a^2 √(3) )/(4) =(12^2 √(3) )/(4) =(144 √(3) )/(4) =36 √(3)`