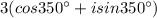Question

Find the cube roots of 27(cos 330Á + i sin 330Á). Please help c:

Answer 1

The cube roots are

`3(cos{110^(\circ)}+isin{110^(\circ)})`

`3(cos{230^(\circ)}+isin{230^(\circ)})`

`3(cos{350^(\circ)}+isin{350^(\circ)})`

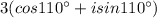
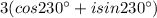
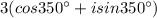
Explanation:

Given the expression 27(cos 330° + i sin 330°)

we have to find the cube roots of the above expression.

By Euler's formula,

`e^(i\theta)=cos{\theta}+isin{\theta`

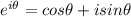
We can write

`cos{330^(\circ)}+isin{330^(\circ)}=e^(330i)`

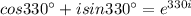
`\sqrt[3]{27(cos{330^(\circ)}+isin{330^(\circ)})}\\\\=\sqrt[3]{3^3(cos{330^(\circ)}+isin{330^(\circ)})}\\\\=\sqrt[3]{3^3(e^(330i))}\\\\=\sqrt[3]{3^3(e^(110i*3))}\\\\=\sqrt[3]{(3e^(110i))^3}\\\\=3e^(110i)=3(cos{110^(\circ)}+isin{110^(\circ)})`

Since, 330°=360°+330°=690° and 330°=2(360°)+330°=1050°

Other two solutions are

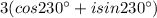`3(cos{230^(\circ)}+isin{230^(\circ)})` and
`3(cos{350^(\circ)}+isin{350^(\circ)})`

Answer 2

Use formula

`e^(ix)=cos(x)+sin(x)`


`\sqrt[3]{27(cos(330^o)+isin(330^o))} \\\sqrt[3]{27e^(i330^o) } \\ \sqrt[3]{27} \sqrt[3]{e^(i330^o)} \\ \sqrt[3]{3^3} \sqrt[3]{e^(i110^o* 3)} \\ \sqrt[3]{3^3} \sqrt[3]{(e^(i110^o))^ 3}} \\ 3e^(i110^o) \\3(cos(110^o)+isin(110^o))`

Since
`330^o=360^o+330^o=690^o` and
`330^o=2* 360^o+330^o=1050^o` there are two more solutions:
1.
`3(cos(230^o)+isin(230^o))`
2.
`3(cos(350^o)+isin(350^o))`