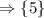Answer:
The equation is given below as
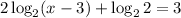
Step 1:
Apply the logarithm law of exponents below
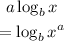
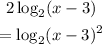
![\begin{gathered} 2\operatorname{\log}_2(x-3)+\operatorname{\log}_22=3 \\ \log_2(x-3)^2+\operatorname{\log}_22=3 \end{gathered}]()
Step 2:
Apply the logarithm law of addition below
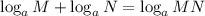
By applying the law, we will have
![\begin{gathered} \operatorname{\log}_2(x-3)^2+\log_22=3 \\ \log_22(x-3)^2=3 \end{gathered}]()
Step 3:
Apply the logarithm principle below
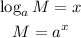
By applying the principle, we will have
![\begin{gathered} \operatorname{\log}_22(x-3)^2=3 \\ 2(x-3)^2=2^3 \\ 2(x-3)^2=8 \\ divide\text{ both sides by 2} \\ (2(x-3)^2)/(2)=(8)/(2) \\ (x-3)^2=4 \end{gathered}]()
Step 4:
Square root both sides and then add 3 to both sides
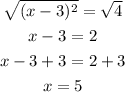
Hence,
The solution set is