Question

(a) How many ordered pairs (x,y) of integers are there such that \sqrt{x^2 + y^2} = 5? Does the question have a geometric interpretation?

(b) How many ordered triples (x,y,z) of integers are there such that \sqrt{x^2 + y^2 + z^2} = 7? Does the question have a geometric interpretation?

Answer 1

a.) Given that
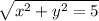
`√(x^2+y^2=5)`, then

`x^2 + y^2 = 5^2 = 25`
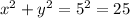
x, y can take the value of-4, -3, 3, 4
Required ordered pairs are (-4, -3), (-4, 3), (-3, -4), (-3, 4), (3, -4), (3, 4), (4, -3), (4, 3).
Therefore, there are 8 ordered pairs (x, y) of integers.

b.) Given that
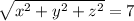
`√(x^2+y^2+z^2)=7`, then

`x^2 + y^2 + z^2 = 7^2 = 49`
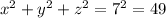
x, y, z can take the value of -6, -3, -2, 2, 3, 6
Required ordered pairs are (-6, -3, -2), (-6, -3, 2), (-6, -2, -3), (-6, -2, 3), (-6, 2, -3), (-6, 2, 3), (-6, 3, -2), (-6, 3, 2) . . .
Therefore, there are 8 x 6 = 48 ordered triples (x, y, z) of integers.