Question

Marty's road-side grill sells hot dogs for $1.25 and hamburgers for $2.50. During a busy summer weekend, he sells a total of 177 hot dogs and hamburgers combined for $363.75. How many hot dogs did he sell? How many hamburgers?

Answer 1

We have to create system of equation
Assume x - number of hot dogs, y - number of hamburgers
We have

`\left \{ {{y+x=177} \atop {1.25x+2.5y=363.75}} \right.`
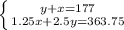
From first equation we get
y+x=177 /-x
y=177-x
Now we can substitute to second eq
1.25x+2.5y=363.75
1.25x+2.5*(177-x)=363.75
1.25x+442.5-2.5x=363.75
-1.25x+442.5=363.75 /-442.5
-1,25x=-78.75 /:(-1.25) divide both sides by -1.25
x=63

Now we can back substitute
y=177-63
y=114
Finally we have

`\left \{ {{y=114} \atop {x=63}} \right.`
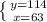
So sold 117 hamburgers and 63 hotdogs