Total spins = 11 + 10 +9 = 30
Total spins of red = 11
Total spins of green = 10
Total spins of blue = 9
The formula for finding probability, P, is

Let the probability of spinning a red be P(R)
Let the probability of spinning a green be P(G)
Let the probability of spinning a blue be P(B)
a) The experimental probability of spinning a green, P(R) is

Hence, the experimental probability of spinning a green is 1/3
b) The experimental probability of spinning a blue, P(B), is

The experimental probability of spinning a blue, P(B), is 3/10
The experimental probability of spinning a green, P(G), is 1/3
The experimental probability of spinning a blue or green, P(B OR G), will be
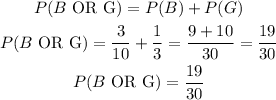
Hence, the experimental probability of spinning a blue or green, P(B OR G) is 19/30
c) The sample space for this experiment is the total possible outcome that can be obtained
Hence, the sample space for this experiment is 30