Question

A local pizzeria offers 11 toppings for their pizzas and you can choose any 5 of them for one fixed price. How many different types of pizzas can you order with 5 toppings?

A. 462

B. 120

C. 55,440

D. 332,640

Answer 1

A.462 is the correct answer. I hope this helps

Answer 2

Answer: Hello mate!

we have 11 toppings, and you can choose 5 of them.

Then the total possible combinations of pizza with 5 toppings is equal to the combinatory number between 11 and 5 (this is because is the same situation where you use first topping A and after topping B, and where you use first topping B and after topping A, for example)

where the combinatory number between A and B is:

`C(A,B) = (A!)/((A-B)!B!)`

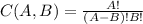
where ,in our case, A is 11 and B is 5.

then we have:

`C(11,5) = (11!)/(6!*5!) = (11*10*9*8*7)/(5*4*3*2) = 11*3*2*7 = 462`

Then the right answer is A = 462, there are 462 pizzas with 5 different toppings from 11 possible ones.