Question

Which is a stretch of an exponential growth function?

a. f(x)=2/3(2/3)^xb. f(x)=3/2(2/3)^xc. f(x)=3/2(3/2)^xd. f(x)=2/3(3/2)^x?

Answer 1

The correct option is C.

Explanation:

The general form of an exponential function is

`f(x)=ab^x`

Where, a is initial value and b is growth factor.

If b>1, then f(x) is a growth function and if 0<b<1, then f(x) is a decay function.

Stretch and compression is defined as

`f(x)=kg(x)`

If |k|>1, then k is stretch factor and if |k|<1, then k is compression factor.

Since the function is stretch of an exponential growth function, therefore the function is in the form of

`f(x)=kb^x`

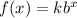
where, b>1 and k>1.

Only in option C,

`k=(3)/(2)>1`

`b=(3)/(2)>1`

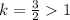
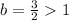
Therefore, the correct option is C.

Answer 2

The answer is C. Hope this helps. :)