In this case, we'll have to carry out several steps to find the solution.
Step 01:
data:
Bank A (single line):
6.5 6.6 6.6 6.7 7.0 7.2 7.5 7.6 7.7 7.7
Bank B (individual lines):
4.1 5.5 5.8 6.2 6.7 7.7 7.7 8.5 9.3 9.9
Step 02:
coefficient of variation:
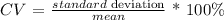
Bank A (single line):
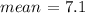
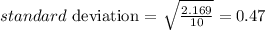

cva = 6.6 %
Bank B (individual lines):
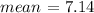
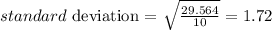
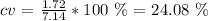
cvb = 24.1 %
Comparison:
cvb > cba
That is the full solution.