Remember that
the average rate of change is equal to
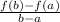
Part 1
we have the interval [-4,-2]
so
a=-4
b=-2
f(a)=f(-2)=(-2)^3-(-2)^2-6(-2)=-8-4+12=0
f(b)=f(-4)=(-4)^3-(-4)^2-6(-4)=-64-16+24=-56
substitute given values
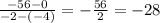
the average rate of change is -28
Part 2
we have the interval [0,1]
a=0
b=1
f(a)=f(0)=(0^3)-(0^2)-6(0)=0
f(b)=f(1)=(1^3)-(1^2)-6(1)=-6
substitute given values
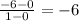
the average rate of change is -6