Question

Consider the function: f(x) = x^3 - x^2 - 6xDetermine the average rate of change in f(x) for each interval. 1. -4 ≤ x ≤ -22. 0 ≤ x ≤ 1

Answer 1

Remember that

the average rate of change is equal to

`(f(b)-f(a))/(b-a)`

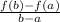
Part 1

we have the interval [-4,-2]

so

a=-4

b=-2

f(a)=f(-2)=(-2)^3-(-2)^2-6(-2)=-8-4+12=0

f(b)=f(-4)=(-4)^3-(-4)^2-6(-4)=-64-16+24=-56

substitute given values

`(-56-0)/(-2-(-4))=-(56)/(2)=-28`

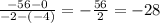
the average rate of change is -28

Part 2

we have the interval [0,1]

a=0

b=1

f(a)=f(0)=(0^3)-(0^2)-6(0)=0

f(b)=f(1)=(1^3)-(1^2)-6(1)=-6

substitute given values

`(-6-0)/(1-0)=-6`

the average rate of change is -6