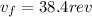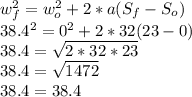Answer:
a). Angular acceleration 32

b). Final angular speed in rpm = 38.4 rpm
Step-by-step explanation:
To calculated angular speed the distance is give 23 revolutions and time of 1.2 minutes so using equations:
a).
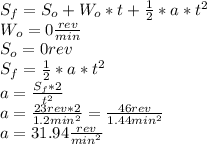
a ≅ 32

b).
 rpm
rpm
Comprobation:
Using a different equation but replacing a= 32
 ,
,
 ,
,
 ,
,