Question

The length of a rectangle is 2 more than thrice its width. The perimeter of the rectangle is 52 cm. Find the area of the rectangle.

Answer 1

Let the length of the rectangle be L

and the width of the rectangle be w

We are told that the length of a rectangle is 2 more than thrice its width.

That is

`\begin{gathered} L=2+(3* w) \\ L=2+3w \end{gathered}`

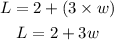
So, the perimeter of the rectangle is 52 cm, and perimeter P of a rectangle is calculated as

`\begin{gathered} P=2(L+w) \\ 52=2(L+w) \end{gathered}`

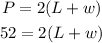
now we will substitute the 2 + 3w for L into the equation, we have

`\begin{gathered} 52=2(L+w) \\ 52=2(2+3w+w) \\ 52=2(2+4w) \\ 52=4+8w \\ 8w=52-4 \\ 8w=48 \\ w=(48)/(8) \\ w=6\text{ cm } \end{gathered}`

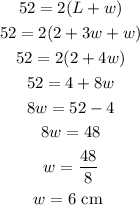
So, the width is 6 cm, the length becomes

`\begin{gathered} L=2+3w \\ L=2+(3*6) \\ L=2+18 \\ L=20cm\text{ } \end{gathered}`

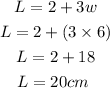
The area A becomes

`\begin{gathered} A=L* w \\ A=20*6 \\ A=120cm^2 \end{gathered}`

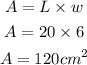
Hence the answer is 120 square centimeters