SOLUTION
Let the length of the rectangle be L
and the width of the rectangle be w
We are told that the length of a rectangle is 2 more than thrice its width.
That is
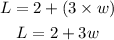
So, the perimeter of the rectangle is 52 cm, and perimeter P of a rectangle is calculated as
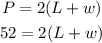
now we will substitute the 2 + 3w for L into the equation, we have
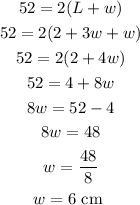
So, the width is 6 cm, the length becomes
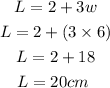
The area A becomes
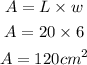
Hence the answer is 120 square centimeters