Given
Cody sold 2 bags of windflower bulbs and 5 bags of daffodil bulbs for a total of $105.
Matt sold 4 bags of windflower bulbs and 3 bags of daffodil bulbs for a total of $91.
Solution
Step 1
Let's bags of windflower be represented by W
Let's bags of daffodil bulbs be represented by D
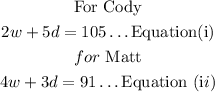
Step 2
Using Substitution method
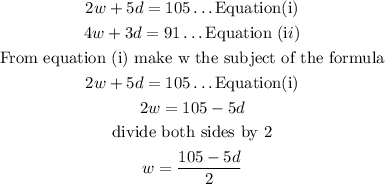
Step 3
We can now substitute to Equation(ii)

Step 4
we can substitute for d in either equation (i) or (ii) to find w

The final answer
one bag of windflower bulbs =$10
one bag of daffodil bag= $17