Question

Lyra and Donna are testing the two-way radios they built for their high school science project. Lyra goes to the top of a building that is 22 meters high with one of the radios and stands directly above the building’s entrance. Donna walks out of the entrance, perpendicular to the building, with the other radio. If Donna is more than 50 meters from the entrance, the connection between the radios breaks. What is the range of communication for the two radios to the nearest meter?

Answer 1

c^2 = a^2 + b^2, and if a = 22 and b = 50, then c is 55

Answer 2

The range of the communication for the two radios is around 55 m.

Explanation:

Consider the provided information.

Lyra goes to the top of a building that is 22 meters high and Donna is more than 50 meters from the entrance,

The required diagram is shown below:

From the figure we can concluded that 2 legs are 22 meters and 50 meters

We need to find the range of radio and we can find the range of radio by finding hypotenuses of the triangle.

Use the Pythagorean theorem to find hypotenuse.

`c^2=a^2+b^2`

`c^2=22^2+50^2`

`c^2=484+2500`

`c^2=2984`

`c=√(2984)`

`c=54.63`

`c\approx 55`

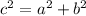
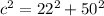
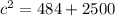
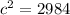
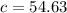
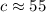
Hence, the range of the communication for the two radios is around 55 m.