We have a graph with a discontinuity and we want to obtain the limit as x tends to 3.
The catch here is that since the function is discontinuous ( is not smooth at 3),
There are 2 limits, one coming from the left and one coming from the right.
We also have the value that the function assumes at 3, which is 7.
Thus, the limit.
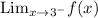
This reads, the limit of f(x) at x = 3 coming from the left side ( that's what the 3 minus means).
If we come to the discontinuity at 3, from the left ( x --> 3 minus) f(x) "approaches" 1 ( it approaches 1, it isn't 1 really, it is 7).
If we were coming from the right side the function would approach 3.
It looks weird that the function looks like it has 3 values at x = 3, but it has only 1.
Therefore
