Question

(A) How high is the ball when it leaves the child’s hand? (B) what is the maximum high or the ball? (C) how far from the child does the ball strike the ground?

Answer 1

Step 1 :

In this question, we are given that the height ( in feet ) of a ball thrown by a child is :

`\begin{gathered} y\text{ =}(-1)/(16)x^2\text{ + 2 x + 3 } \\ \text{where x is the horizontal distance in f}eet\text{ from the point at which } \\ the\text{ ball is thrown} \end{gathered}`

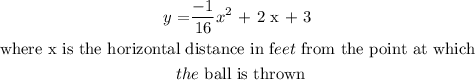
Step 2 :

a) How high is the ball when it leaves the child's hand?

Answer:

`\begin{gathered} \text{Given y = }(-1)/(16)x^2\text{ + 2 x + 3 } \\ \text{when it leaves the child's hand, x = 0} \\ y\text{ = }(-1)/(16)(0)^2\text{ + 2 ( 0 ) + 3 } \\ y\text{ = 3 f}eet \end{gathered}`

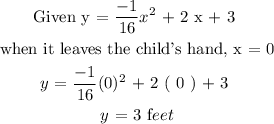
b) What is the maximum height of the ball?

Answer:

`\begin{gathered} \frac{d\text{ y}}{d\text{ x}}\text{ = }(-1)/(8)\text{ x + 2 = 0} \\ (-1)/(8)x\text{ = - 2} \\ (x)/(8)\text{ = 2 } \\ \text{x = 2 x 8} \\ x\text{ = 16 f}eet \\ \text{Put x = 16 into the equation:} \\ y\text{ = }(-1)/(16)x^2\text{ + 2 x + 3 } \\ y\text{ = }(-1)/(16)(16)^2\text{ + 2 ( 16 ) + 3 } \\ y\text{ = -16 + 32 + 3 } \\ y\text{ ( Ma}\xi mum\text{ Height ) = 19 fe}et \end{gathered}`

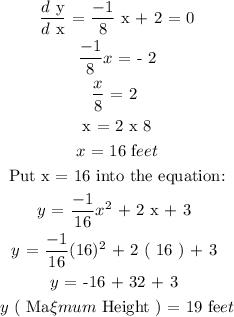
c) How far from the child does the ball strike the ground?

`\begin{gathered} \text{Given y = }(-1)/(16)x^2\text{ + 2 x + 3 } \\ \text{Set y = 0, we have that:} \\ (-1)/(16)x^2\text{ + 2 x + 3 = 0} \\ \text{Multiply both sides by 16, we have that:} \\ -x^2\text{ + 32 x + 48 = 0} \\ x^2\text{ - 32 x - 48 = 0} \\ \text{The values of x are: -1. 436 or 33. 436} \\ we\text{ ignore x = - 1. 436 ( since it is negative )} \end{gathered}`

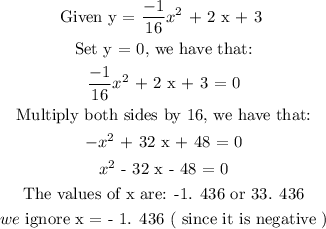
But the child threw the ball from x = 0,

It means that the ball landed 33. 436 feet away from the child.