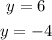The line segment connects the point (-5, 1) and (7, y), the segment has a length of 13 units. This is the distance between the points.
The equation for the distance of two points A and B, is:

Then, taking A = (-5, 1) and B = (7, y)
We can write:
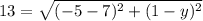
Then, we can apply the square on both sides and solve the parentheses:
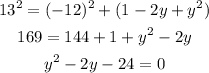
Now we can apply the quadratic formula:
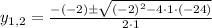

The two solution are:
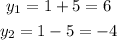
Then, the two answers are: