Question

Solve the following system of equations by graphing and select the correct answer below:

2x + 6y = 20
3x _ 2y = 8


Answers:
x = 4, y = 2
x = 4, y = _2
x = _2, y = 4
x = 2, y = 4

Answer 1

Option A is correct.

x =4 , y = 2

Step-by-step explanation:

Given the system of equation:

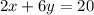`2x+6y = 20` ......[1]

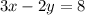`3x-2y = 8` .....[2]

Multiply equation [2] by 3 both sides we get;

`3 \cdot (3x-2y) = 3 \cdot 8`

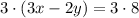
Using distributive property:
`a\cdot (b+c) = a\cdot b+ a\cdot c`

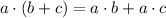
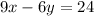`9x - 6y = 24` .....[3]

Add equation [1] and [3], to get eliminate y we get;

`2x+6y+9x-6y= 20+24`

Combine like terms we have;

`11x = 44`

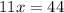
Divide both sides by 11 we get;

`x = 4`

Substitute the value of x =4 in [1] we get;

2(4) + 6y = 20

8 + 6y = 20

Subtract 8 from both sides we have;

6y = 12

Divide both sides by 6 we have;

y = 2

Therefore, the values of x and y are; 4 and 2.

Answer 2

the only answer is x = 4, y = 2,
2(4) + 6(2) = 20
3(4) _ 2(2) = 8
the graph is so easy, please try!!