Question

In AOPQ, the measure of XQ=90°, OP = 96 feet, and PQ = 23 feet l'ind the measure of 20 to the nearest degree.

Answer 1

Given the triangle OPQ:

`\begin{gathered} m\angle Q=90 \\ OP=96ft \\ PQ=23ft \end{gathered}`

We need to find the measure of angle O

So,

As angle Q = 90, so, the hypotenuse is the side OP

The side PQ represents the opposite side to the angle O

so,

`\begin{gathered} \sin O=(opposite)/(hypotenuse) \\ \\ \sin O=(PQ)/(OP)=(23)/(96) \\ \\ m\angle O=\sin ^(-1)(23)/(96)\approx13.86 \end{gathered}`

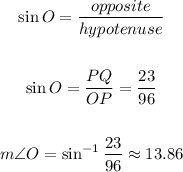
Rounding to the nearest degree:

So, the answer will be: the measure of angle O = 14