Question

The volumes of two similar solids are 8 ft3 and 125 ft3. The surface area of the smaller solid is 4 ft2. What is the surface area of the larger solid?

Answer 1

25 square feet

Explanation:

We are given that

Volume of smaller solid= 8 cubic feet

Volume of large solid=125 cubic feet

Surface area of smaller solid=4 square feet

We have to find the surface area of larger solid.

Volume of is a cubic function

Ratio of two solids=6:125

`(V_1)/(V_2)=(2^3)/(5^3)=(a^3)/(b^3)`

`(a)/(b)=(2)/(5)`

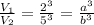
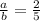
Where a= Side of small solid

b=Side of large solid

Ratio of corresponding sides of two solids=2:5

When two solids are similar then the ratio of surface area

`(Area\;of\;small\;solids)/(area\;of\;larger\;solids)=(a^2)/(b^2)`

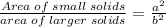
Area of small solid: area of larger solid=
`(2^2)/(5^2)`

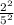
4: area of large solid=4: 25

Area of larger solid=
`(4* 25)/(4)=25 ft^2`

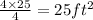
Hence, the area of larger solid=25 square feet

Answer 2

Surface area of larger solid is = 25 square feet.

Explanation:

Given that,

Volume of smaller solid = 8 cubic feet

Volume of larger solid = 125 cubic feet

We know that,

Volume is the function of cube of dimensions.

and area is the function of square of dimensions.

So,

8 = 2³

125 = 5³

Ratio of sides = 2 : 5

Ratio of surface area = 4:x (let surface area of larger solid x)

So,

`(4)/(x)=(2^(2) )/(5^(2) )`

x = 25 sq ft

surface area of the larger solid = 25 sq ft

That's the final answer.