Question

Which equation is a point slope form equation for line AB ?

A.y−2=−2(x+6)y−2=−2(x+6)

B.y−6=−2(x+2)y−6=−2(x+2)

C.y−2=−2(x+2)y−2=−2(x+2)

D.y−2=2(x+2)

Answer 1

Answer: the answer is B... short answer but correct

Explanation:

Answer 2

Step 1

Find the equation of the line AB

we know that

the equation of the line into point-slope form is equal to

`y-y1=m(x-x1)`

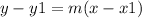
Let

`A( -2,6)\\B(2,-2)`

Find the slope m

we know that

the slope between two points is equal to

`m=((y2-y1))/((x2-x1))`

substitute

`m=((-2-6))/((2+2))`

`m=((-8))/((4))`

`m=-2`

with the slope m and point A find the equation of the line AB

`y-6=-2(x+2)`

or

with the slope m and point B find the equation of the line AB

`y+2=-2(x-2)`

we will proceed to verify each case to determine the solution of the problem

Step 2

Verify case A

Case A)
`y-2=-2(x+6)`

the slope of the line is
`m=-2`

but the point
`(-6,2)` -----> not lie on the line AB (see the graph)

therefore

the case A is not the solution

Step 3

Verify case B

Case B)
`y-6=-2(x+2)`

the slope of the line is
`m=-2`

and the point
`(-2,6)` -----> is the point A

therefore

the case B is a solution

Step 4

Verify case C

Case C)
`y-2=-2(x+2)`

the slope of the line is
`m=-2`

but the point
`(-2,2)` -----> not lie on the line AB (see the graph)

therefore

the case C is not the solution

Step 5

Verify case D

Case D)
`y-2=2(x+2)`

the slope of the line is
`m=2` -----> the slope is not equal to the slope AB

and the point
`(-2,2)` -----> not lie on the line AB (see the graph)

therefore

the case D is not the solution

the answer is

The equation
`y-6=-2(x+2)` is a point-slope form of the line AB