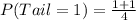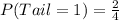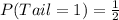Question

When a penny is flipped two times, the probability of flipping exactly one tail is__?

Answer 1

`P(Tail = 1) = (1)/(2)`

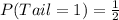
Explanation:

Given

`Flips = 2`

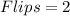
Required

Probability of exactly one tail

This event can be represented as:

(Head and Tail) or (Tail and Head)

In the flip of a coin (penny), the following probabilities exist:

`P(Head) = (1)/(2)`

`P(Tail) = (1)/(2)`

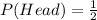
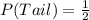
So, the required probability is:

`P(Tail = 1) = (P(Head) * P(Tail)) + (P(Tail) * P(Head))`

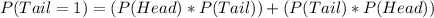
Substitute values for P(Head) and P(Tail)

`P(Tail = 1) = ((1)/(2)*(1)/(2)) + ((1)/(2)*(1)/(2))`

`P(Tail = 1) = ((1)/(4)) + ((1)/(4))`

`P(Tail = 1) = (1)/(4) + (1)/(4)`

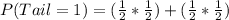
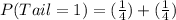
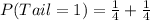
Take LCM

`P(Tail = 1) = (1+1)/(4)`

`P(Tail = 1) = (2)/(4)`

`P(Tail = 1) = (1)/(2)`