Question

If points A(4,5), B(1,1) and C (-2,5) are vertices of an isosceles triangle, determine measure of each base angle (in degrees with 2 decimal places);

Answer 1

53.13 degrees.

Step-by-step explanation:

Given the vertices of ABC: A(4,5), B(1,1) and C (-2,5)

First, determine the side lengths AB, AC, and BC using the distance formula:

`\begin{gathered} Distance=√((x_2-x_1)^2+(y_2-y_1)^2) \\ AB=\sqrt[]{(4-1)^2+(5-1)^2}=\sqrt[]{(3)^2+(4)^2}=\sqrt[]{25}=5 \\ AC=\sqrt[]{(4-(-2))^2+(5-5)^2}=\sqrt[]{(6)^2}=6 \\ BC=\sqrt[]{(1-(-2))^2+(1-5)^2}=\sqrt[]{(3)^2+(-4)^2}=\sqrt[]{25}=5 \end{gathered}`

A rough sketch of the triangle is attached below:

The base angles of the Isosceles triangle are angles A and C.

Next, we find the value of angle A using the Law of Cosine.

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ 5^2=6^2+5^2-(2*6*5)\cos A \\ 25=61-60\cos A \\ -60\cos A=25-61=-36 \\ \cos A=(-36)/(-60) \\ A=\arccos ((36)/(60)) \\ A\approx53.13\degree \end{gathered}`

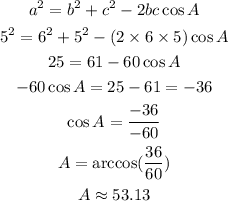
The measure of each base angle is 53.13 degrees (correct to 2 decimal places).

CHECK