Question

Write a system of equations to describe the situation below, solve using an augmented matrix.The drama club is selling gift baskets to raise money for new costumes. During the fall play, they sold a combined 19 regular gift baskets and 2 deluxe gift baskets, earning a total of $451. During the spring musical, they sold 1 deluxe gift basket, earning a total of $45. How much are they charging for the different sized gift baskets?The drama club is charging $? for a regular gift basket and $? for a delexue gift basket.

Answer 1

Regular gift basket = $19

Deluxe gift basket = $45

Explanation:

We have the following:

x : cost of a regular gift basket

y : cost of a deluxe gift basket

With the data from the statement we create the augmented matrix:

`\begin{pmatrix}19&2\\ \:\:0&1\end{pmatrix}\begin{pmatrix}x\\ \:y\end{pmatrix}=\begin{pmatrix}451\\ \:\:45\end{pmatrix}`

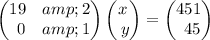
We solve the matrix, like this:

`\begin{gathered} \begin{pmatrix}19x+2y \\ 0\cdot\:x+1\cdot\:y\end{pmatrix}=\begin{pmatrix}19x+2y \\ y\end{pmatrix} \\ \\ \begin{pmatrix}19x+2y \\ y\end{pmatrix}=\begin{pmatrix}451 \\ 45\end{pmatrix} \\ \\ \begin{bmatrix}19x+2y=451\\ y=45\end{bmatrix} \\ \\ \begin{bmatrix}19x+2\cdot45=451\end{bmatrix}\rightarrow\begin{bmatrix}19x+90=451\end{bmatrix}\rightarrow\begin{bmatrix}19x=451-90\end{bmatrix}\rightarrow\begin{bmatrix}x=(361)/(19)\end{bmatrix}\rightarrow\begin{bmatrix}x=19\end{bmatrix} \\ \\ \begin{bmatrix}x=19 \\ y=45\end{bmatrix} \end{gathered}`

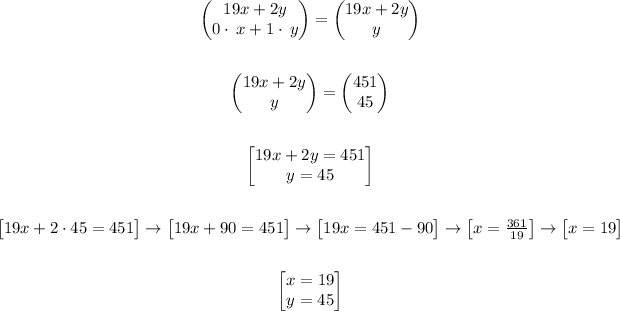
Therefore,

The drama club is charging $19 for a regular gift basket and $45 for a deluxe gift basket.