Question

Which table represents viable solutions for y = 5x, where x is the number of tickets sold for the school play and y is the amount of money collected for the tickets?

Answer 1

The answer is the first table: (0, 0), (10, 50), (51, 255), (400, 2000)

Our function is y = 5x

Let's check all of the tables:
Table 1:
x = 0, y = 0 ⇒ 0 = 5 · 0 ⇒ 0 = 0
x = 10, y = 50 ⇒ 50 = 5 · 10 ⇒ 50 = 50
x = 51, y = 255 ⇒ 255 = 5 · 51 ⇒ 255 = 255
x = 400, y = 2000 ⇒ 2000 = 5 · 400 ⇒ 2000 = 2000

Since all calculations from the first table are correct, we can conclude that the first table represents viable solutions. Also, if you check it out, the third table gives all correct calculations for the function y = 5x, however, its solutions cannot be viable because the number of sold tickets and collected money cannot be negative numbers

Answer 2

For this case we have the following equation:

`y = 5x`
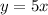
Where,
x: he number of tickets sold
y: the amount of money collected for the tickets
The domain of the function must be:

`x \geq 0`
Therefore, we must find a table that complies with this restriction and also have the corresponding values for x and y.
The first table complies with the restriction and has correct values for the variables:
x y
0 0
10 50
51 255
400 2000

Answer:
First table