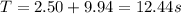Question

At time t=0 a grinding wheel has an angular velocity of 26.0 rad/s. It has a constant angular acceleration of 25.0 rad/s^2 until a circuit breaker trips at time t = 2.50 s. From then on, the wheel turns through an angle of 440 rad as it coasts to a stop at constant angular deceleration.

Through what total angle did the wheel turn between t=0 and the time it stopped? At what time does the wheel stop? What was the wheel's angular acceleration as it slowed down?

Answer 1

The equations of motions will be applied in this question; except that in this case it will be angular motion instead of linear motion.
We use the formula
v = u + at; to determine the final velocity of before the circuit breaker trips.
v = 26 + 2.5 x 25
= 88.5 rad/s
Total angle covered before circuit breaker trips:
2as = v² - u²
s = (88.5² - 26²)/2(25)
s = 143.125 rad
Angle covered before stopping after trip = 440 rad
Total angle covered from start to finish:
143.125 + 440
= 583.125 rad

Acceleration as wheel stops:
2as = v² - u²; v = 0
a = -(88.5²)/2(440)
a = 0.1 rad/s²

Time to stop:
v = u + at
0 = 88.5 - 0.1t
t = 885 seconds
Total time: 2.5 + 885
= 887.5 seconds

Answer 2

Angle turned by the wheel is given by the kinematics as

`\theta = \omega t + (1)/(2)\alpha t^2`

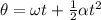
now here we know that

`\omega = 26 rad/s`

`\alpha = 25 rad/s^2`

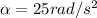
t = 2.50 seconds

`\theta = 26(2.50) + (1)/(2)(25)(2.50)^2`

`\theta = 143.1 rad`

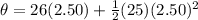
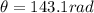
So here total angle that the wheel turn is given as

`\theta = 143.1 + 440 = 583.1 rad`

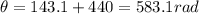
Speed of the wheel after 2.5 s

`\omega = \omega_0 + \alpha t`

`\omega = 26 + (25)(2.5)`

`\omega = 88.5 rad/s`

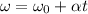
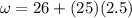
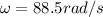
now angular deceleration is given as

`\alpha_1 = (\omega^2 - \omega_0^2)/(2\theta)`

`\alpha_1 = (0 - 88.5^2)/(2(440))`

`\alpha_1 = -8.9 rad/s^2`

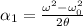
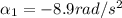
time taken to stop

`t = (\omega - \omega_0)/(\alpha)`

`t = (0 - 88.5)/(-8.9) = 9.94 s`

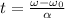
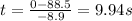
now total time is given as

`T = 2.50 + 9.94 = 12.44 s`