Question

Three sides of a fence and an existing wall form a rectangular enclosure. The total length of a fence used for the three sides is 240 ft. Let x be the length of two sides perpendicular to the wall as shown. Write an equation of area A of the enclosure as a function of the length x of the rectangular area. Then find the value(s) of x for which the area is 5500 ft^2.

__________________ I I x I I x _________________________ Existing Wall X is the shorter wall. The existing wall is longer than the one across from it, I tried to make it look like that in the picture.

Answer 1

Let the wall's length be y. So the fence parallel is also y.

We form the equation;
2x + y = 240

Now the area A is x*y, which is given as 5500.

We have 2 equations with 2 variables. Solve them and get the answer.

xy = 5500
2x + y = 240

Y = 5500/x

2x + (5500/x) = 240
2x^2 - 240x + 5500 = 0
x^2 - 120x + 2750 = 0
Work out the value(s) of x from above.

Answer 2

values of x = 30.85, 89.16 ft

Explanation:

Let length of two sides perpendicular to the wall be x ft and length of the wall is y ft.

area A of the enclosure will be A = xy

Since area of the enclosure = 500 square feet

xy = 5500 ------(1)

Length of the three sides has been given as 240 ft.

2x + y = 240

y = 240 - 2x ------(2)

Now we put the value of y from equation 2 to equation 1

x(240 - 2x) = 5500

240x - 2x² = 5500

Now we divide this equation by 2

120x - x² = 2750

x² - 120x = - 2750

x² - 120x + 2750 = 0

x =
`\frac{120\pm \sqrt{(-120)^(2)-4(1)(2750)}}{2}`

=
`(120\pm √(14400-11000))/(2)`

=
`(120\pm √(3400))/(2)`

=
`(120\pm 58.31)/(2)`

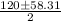
x = 30.85, 89.16 ft

y = 178.28, 61.69 ft

If the wall is shorter than other sides then the value of x will be 89.16.