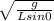Question

An object of mass m swings in a horizontal circle on a string of length L that tilts downward at angle θ.

Find an expression for the angular velocity ω in terms of g, L and angle θ.

Answer 1

Let g, r, L and T are gravity, radius, length, and angle of string w/r/t vertical, respectively.
Then
ω²r = rg/Lcos T
ω² = g/L cos T
ω = √(g / L cos T)

Answer 2

The expression would be ω =
`\sqrt{(g)/(L sin 0 ) }`

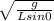
Step-by-step explanation:

Given that ω is the angular velocity

g is the acceleration due to gravity

L is the length

θ is the angle of downward tilt

For an object we compare the horizontal and vertical component of the forces acting on the body;

For vertical component

T sinθ = mg............1

For the horizontal component

T cos θ =
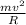`(mv^(2) )/(R)` .............2

R is our radius and is = L cos θ

v = ωR

substituting into equation 2 we have

T cos θ = m(ωR
`)^(2)` /R

T cos θ=m(ω
`)^(2)`R ..................3

Now comparing the vertical and the horizontal component we have;

equation 1 divided by equation 3 we have

T sin θ /T cos θ = mg / m(ω
`)^(2)`R

Tan θ = g / (ω
`)^(2)`R............4

Making ω the subject formula we have;

(ω
`)^(2)` = g/ R Tan θ

But R = L cos θ and Tan θ = sin θ/ cosθ

putting into equation 4 we have;

(ω
`)^(2)` = g /[( L cos θ) x( sin θ/ cosθ)]

(ω
`)^(2)` = g/ L sinθ

ω =
`\sqrt{(g)/(L sin 0 ) }`

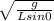
Therefor the expression for the angular velocity ω in terms of g, L and angle θ would be ω =
`\sqrt{(g)/(L sin 0 ) }`