Question

How many photons are produced in a laser pulse of 0.497 J at 469 nm?

Answer 1

E=hν where E is the energy of a single photon, and ν is the frequency of a single photon. We recall that a photon traveling at the speed of light c and a frequency ν will have a wavelength λ given by λ=cνλ will have an energy given by E=hcλλ=657 nm. This will be E=(6.626×10−34)(2.998×108)(657×10−9)=3.0235×10−19J So we now know the energy of one photon of wavelength 657 nm. To find out how many photons are in a laser pulse of 0.363 Joules, we simply divide the pulse energy by the photon energy or N=Epulse Ephoton=0.3633.0235×10−19=1.2×1018So there would be 1.2×1018 photons of wavelength 657 nm in a pulse of laser light of energy 0.363 Joules.

Answer 2

`1.1702* 10^(18)`photons are produced in a laser pulse of 0.497 Joules at 469 nm.

Step-by-step explanation:

Energy of the laser pulse ,E'= 0.497 J

Number of photons = n

Energy of 1 photon with 469 nm wavelength = E

E' = n × E

`E=(hc)/(\lambda )`

h = Planck's constant =
`6.626* 10^(-34)Js`

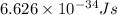
c = speed of light =
`3* 10^8m/s`

`\lambda` = wavelength =
`469 nm=469* 10^(-9)m`

`1 nm=10^(-9) m`

Now put all the given values in the above formula, we get the energy of the photons.

`E=(6.626* 10^(-34)Js* 3* 10^8m/s)/(469* 10^(-9)m)=4.2384* 10^(-19) J`

`n=(E')/(E)`

`n=(0.496 J)/(4.2384* 10^(-19) J)=1.1702* 10^(18) photons`

`1.1702* 10^(18)`photons are produced in a laser pulse of 0.497 Joules at 469 nm.