The general equation of a line is given as
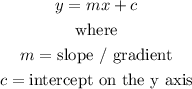
Two lines are said to be parallel when they have the same slope or gradient that is
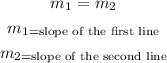
The equation of the line given is
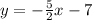
By comparing coefficients,
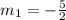
So from the options, we will figures out the equation that has the same gradient as -5/2
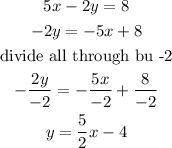
The slope above is 5/2 therefore the option A is not parallel to the line
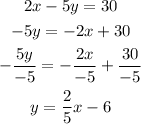
The slope above is 2/5 therefore Option B is not parallel to the line also
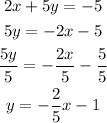
The slope above is -2/5 Therefore Option C is also not parallel to the line
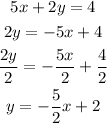
The slope above is -5/2 which is the same as the slope in the question
Therefore,
The correct answer is OPTION D