Question

Which of the following is the conjugate of a complex number with 5 as the real part and −2i as the imaginary part?

Answers:

5 + 2i

−5 − 2i

−5 + 2i

5 − 2i

Answer 1

5+2i. You only have to change the operation of the original expression, not the signs (positives and negatives) of each term.

Answer 2

Answer: the correct option is

(A) 5 + 2i.

Step-by-step explanation: We are given to select the complex number that is the conjugate of a complex number with 5 as the real part and −2i as the imaginary part.

We know that

a complex number z can be written as

z = a + bi, where a is the real part and bi is the imaginary part.

According to the given information, we have

a = 5 and b = -2i

So, z = 5 - 2i.

Therefore, the conjugate of z is given by

`\bar{z}=5+2i.`

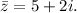
Thus, the required conjugate number is 5 + 2i.

Option (A) is CORRECT.