Answer:
The values of
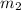 and
and
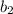 that will create a system of linear equations with no solution are
that will create a system of linear equations with no solution are
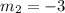 and
and
 .
.
Explanation:
An example of a system of linear equations are two lines parallel to each other. In other words, there are two lines such that:
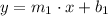 (1)
(1)
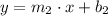 (2)
(2)
Where:
 - Independent variable.
- Independent variable.
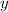 - Dependent variable.
- Dependent variable.
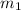 ,
,
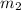 - Slope.
- Slope.
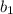 ,
,
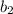 - y-Intercept.
- y-Intercept.
If both lines are parallel to each other, then we must observe these two conditions:
1)
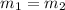
2)
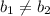
Therefore, the values of
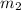 and
and
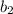 that will create a system of linear equations with no solution are
that will create a system of linear equations with no solution are
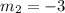 and
and
 .
.