Question

A circle has a diameter of 4 inches. Which statement about the area and circumference of the circle is true?

The Answers:
A- A comparison of the area and circumference of the circle is not possible because there is not enough information to find both.
B- The numerical values of the circumference and area are equal.
C- The numerical value of the circumference is greater than the numerical value of the area.
D- The numerical value of the circumference is less than the numerical value of the area.

BTW it's not A

Answer 1

area = pi × 2^2
= 4pi

circumference = 2 × pi × 2
= 4pi

the answer is b

Answer 2

Option B is correct

The numerical values of the circumference and area are equal.

Explanation:

Circumference(C) and Area (A)of the circle is given by:

`C = 2\pi r` ....[1]

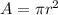`A = \pi r^2` ......[2]

where, r is the radius of the circle.

As per the statement:

A circle has a diameter of 4 inches.

We know:

Diameter = 2 (radius(r))

then;

4 = 2r

Divide both sides by 2 we have;

r = 2 inches

Substitute these in [1] and [2] we have;

Use
`\pi = 3.14`

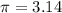
then;

`C = 2 \cdot 3.14 \cdot 2 = 12.56 in.`

`A = 3.14 \cdot 2^2 = 3.14 \cdot 4 = 12.56 in^2`

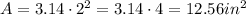
Therefore, the numerical values of the circumference and area are equal i.e 12.56